Bayes Theorem: Making Good Decisions with Incomplete Data

Today, privacy laws and user consent directly affect the quality of digital data processing. Although Google enables data collection taking into account users' cookie permissions through Consent Mode, regulations sometimes prevent us from directly accessing the actual data.

Although Consent Mode cannot directly collect data from users who do not give cookie consent, Bayes' Theorem compensates for this. Google Analytics 4 predicts missing conversions and user interactions with statistical methods such as Bayes Theorem.

In this article, I will discuss how the Bayes Theorem works in GA4 and the reliability of Bayesian modeling.

Data Loss in Consent Mode and GA4

Consent Mode changes the way GA4 collects data according to whether users give cookie consent. For users who give cookie consent, GA4 collects all data and records user behavior in full. However, for users who do not grant cookie permission, GA4 cannot collect most of the data; only anonymous data and limited interactions are recorded.

These data gaps are filled with modeling techniques. GA4 uses statistical methods such as the Bayes Theorem to fill in these missing data.

Bayes Theorem and its Role in GA4

Bayes' Theorem explains how the probability of an event changes depending on the likelihood of another event occurring. This theorem allows probability calculations to be made by taking into account the possibility of this event and the probability of other events depending on it, especially in the case of the occurrence of an event.

Bayes' Theorem works as follows:

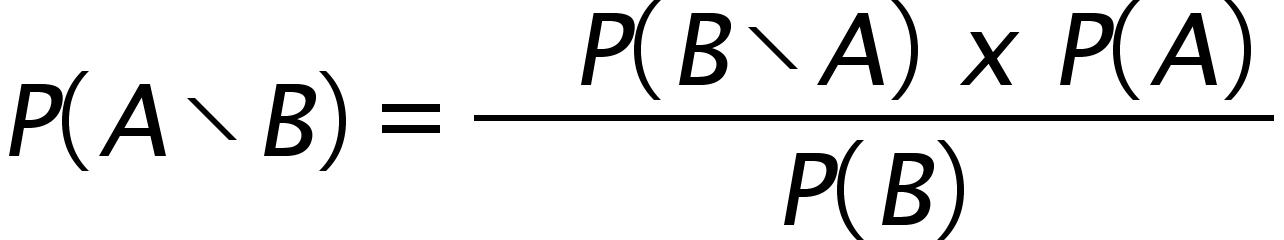
P(A \ B) = probability of A occurring under condition B.

P(B \ A) = probability of B occurring under condition A.

P(A) = the predicted probability of A.

P(B) = the overall probability of B.

Bayesian Modeling with Example

Let's say you have an e-commerce site and you attract users to your site with ads. According to your data:

• 20% of users allow cookies to be converted.
• The conversion rate of users who do not allow cookies is only 5% due to incomplete measurement.
• 40% of users allow cookies, 60% do not.
• There is a 50% chance that a user who converts does not allow cookies.
• The overall conversion rate is 8%.

What is the probability that a user who does not give cookie consent will convert?

Step 1: Determine Conversion Rates for Users with and without Cookie Consent

P(Conversion | Cookie Consent) = 0.20 (Conversion Rate of Cookie Consenting Users)

P(Conversion | No Cookie Consent) = 0.05 (Conversion Rate of Users Not Allowing Cookies)

We will also consider the proportion of website traffic for both groups:

P(Cookie Consent) = 0.40 (Impact of Cookie Consenting Users on Overall Traffic)

P(No Cookie Consent) = 0.60 (Impact of No Cookie Consent Users on Overall Traffic)

Step 2: Calculate the Probability of Conversion Using Bayes Theorem

Using Bayes' Theorem, let's calculate the probability of conversion for users who do not give cookie permission.

First, we need to be aware of the possibility that a user who converts does not give cookie consent. Let's take this probability as 50%:

P(Cookie Permission Not Allowed | Conversion) = 0.50

We must also consider the possibility of general transformation:

P(Conversion) = 0.08 (Overall Conversion Rate)

The rate of users who do not allow cookies is 60%:

P(No Cookie Consent) = 0.60

Now, let's apply Bayes' Theorem with this data:

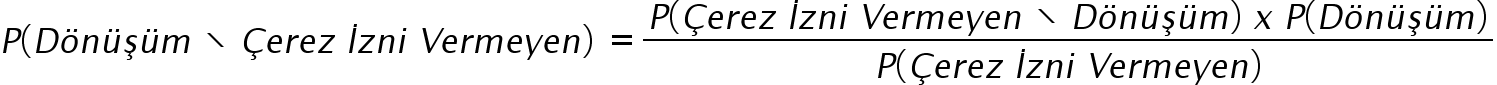
With the data here, the calculation will be as follows:

As a result, users who do not grant cookie consent have a 6.67% probability of converting.

Reliability of GA4 and Bayesian Modeling

Google Analytics 4 completes missing data using statistical and machine learning methods such as Bayesian modeling. However, the reliability of Bayesian modeling and data modeling processes depends on some important factors.

Size and Quality of Data Sets

Bayesian modeling is based on learning from historical data. Therefore, the quality and size of the data used in GA4's modeling processes play a critical role in the reliability of the modeling results.

• Big Data Sets: GA4 works with extensive user data collected over many years. These large data sets increase the accuracy of the model because predictions made over many samples and cases are more reliable.
• Data Diversity: GA4 combines data from different user segments, device types, geographic locations, and demographics. This diversity enables the model to generalize, meaning it can make valid predictions in different scenarios.

Machine Learning and Continuously Updated Modeling

GA4 not only uses static Bayes formulas but also brings machine learning algorithms into play. This ensures that the modeling processes are constantly evolving and re-optimized.

Machine learning learns the patterns in the data set over time and the model updates itself as the data changes. If the conversion rate of a user segment changes over time, the model adapts accordingly.

Tested and Verified Results

Google conducts continuous validations on different user groups to test the reliability of predictions made by methods such as Bayesian modeling. Modeling results are compared to real-world user behavior and the accuracy of the model is measured based on these comparisons.

• A/B Tests and Test Groups: After modeling the data, GA4 validates these predictions in test groups. For example, conversion predictions made for users who do not allow cookies are then compared with actual conversion data.
• Consolidation and Refinement: The results from these tests are used to refine GA4's modeling algorithms.

Bayesian Modeling and Margin of Error Calculation

The reliability of Bayesian modeling is related to the accuracy of the estimated probabilities. With Bayesian modeling, GA4 not only makes a single prediction but also calculates the possible margins of error.

While Bayesian modeling works on the probabilities of events, it also calculates the uncertainty level of the model. GA4 explicitly specifies the reliability of forecasts with statistical confidence intervals.

• Confidence Interval: Results calculated with Bayesian modeling usually include a confidence interval, which indicates the model's accuracy and reliability.
• Margin of Error: GA4 shows the user that the model is only guessing and may not always give accurate results.